Question 8.104

\( W = [0,1] \times [0,1] \times [0,1] \textbf{F} = x \textbf{i} + y \textbf{j} + z \textbf{k}\)

Question 8.105

\(W\) as in Exercise 1, and \(\textbf{F} = zy \textbf{i} + xz \textbf{j} + xy \textbf{k}\)

Question 8.106

\( W = \{ (x,y,z) : x^2 + y^2 + z^2 \leq 1 \}\) \quad (the unit ball), \(\textbf{F} = x \textbf{i} + y \textbf{j} + z \textbf{k}\)

Question 8.107

\(W\) as in Exercise 3, and \(\textbf{F} = -y \textbf{i} + x \textbf{j} + z \textbf{k}\)

Question 8.108

Use the divergence theorem to calculate the flux of \({\bf F} = (x-y) {\bf i} + (y -z) {\bf j} + (z-x){\bf k}\) out of the unit sphere.

Question 8.109

Let \({\bf F}=x^3{\bf i}+y^3{\bf j}+z^3{\bf k}\). Evaluate the surface integral of \({\bf F}\) over the unit sphere.

Question 8.110

Evaluate \({\intop\!\!\!\intop}_{\partial\! W}{\bf F}\,{\cdot}\,{\,d} {\bf S}\), where \({\bf F}=x{\bf i}+y{\bf j}+z{\bf k}\) and \(W\) is the unit cube (in the first octant). Perform the calculation directly and check by using the divergence theorem.

Question 8.111

Repeat Exercise 7 for

• (a) \({\bf F}={\bf i}+{\bf j}+{\bf k}\)
• (b) \({\bf F}=x^2{\bf i} +x^2{\bf j} +z^2{\bf k}\)

Question 8.112

Let \({\bf F}=y{\bf i} +z{\bf j} +xz{\bf k}\). Evaluate \({\intop\!\!\!\intop}_{\partial\! W}{\bf F}\,{\cdot}\,{\,d} {\bf S}\) for each of the following regions \(W\):

• (a) \(x^2+y^2\leq z\leq 1\)
• (b) \(x^2+y^2\leq z\leq 1\) and \(x\geq 0\)
• (c) \(x^2+y^2\leq z\leq 1\) and \(x\leq 0\)

Question 8.113

Repeat Exercise 9 for \({\bf F}=(x-y){\bf i}+(y-z){\bf j}+ (z-x){\bf k}\). [The solution to part (b) only is in the Study Guide to this text.]

Question 8.114

Find the flux of the vector field \({\bf F}= (x-y^2){\bf i} + y{\bf j} + x^3 {\bf k}\) out of the rectangular solid \([0,1] \times [1,2] \times [1,4]\).

Question 8.115

Evaluate \({\intop\!\!\!\intop}_S{\bf F}\,{\cdot}\,{\,d} {\bf S}\), where \({\bf F}=3xy^2{\bf i}+3x^2y{\bf j}+z^3{\bf k}\) and \(S\) is the surface of the unit sphere.

Question 8.116

Let \(W\) be the pyramid with top vertex \((0,0,1)\), and base vertices at \((0,0,0)\), \((1,0,0)\), \((0,1,0)\), and \((1,1,0)\). Let \(S\) be the two-dimensional closed surface bounding \(W\), oriented outward from \(W\). Use Gauss’ theorem to calculate \({\intop\!\!\!\intop}_{S} \textbf{F} \cdot d \textbf{S}\), where: \[ \textbf{F}(x,y,z) = (x^2 y, 3y^2 z, 9z^2 x). \]

Question 8.117

Let \(W\) be the three-dimensional solid enclosed by the surfaces \(x = y^2\), \(x=9\), \(z=0\), and \(x=z\). Let \(S\) be the boundary of \(W\). Use Gauss’ theorem to find the flux of \(\textbf{F}(x,y,z) = (3x - 5y)i + (4z - 2y)j + (8yz)k\) across \(S\): \({\intop\!\!\!\intop}_{S} \textbf{F} \cdot d \textbf{S}\).

Question 8.118

Evaluate \({\intop\!\!\!\intop}_{\partial\! W} {\bf F} {\,{\cdot}\,} {\bf n} {\,d} A\), where \({\bf F}(x,y,z) = x{\bf i} + y{\bf j} - z{\bf k}\) and \(W\) is the unit cube in the first octant. Perform the calculation directly and check by using the divergence theorem.

Question 8.119

Evaluate the surface integral \({\intop\!\!\!\intop}_{\partial S} {\bf F} {\,{\cdot}\,} {\bf n} {\,d} A\), where \({\bf F}(x,y,z) = {\bf i} + {\bf j} + z(x^2 + y^2)^2{\bf k}\) and \(\partial\! S\) is the surface of the cylinder \(x^2 + y^2 \le 1, 0\le z \le 1\).

Question 8.120

Prove that \begin{eqnarray*} \intop\!\!\!\intop\!\!\!\intop\nolimits_{W} ({\nabla}\!f) \,{\cdot}\, {\bf F} {\it {\,d} x}\, {\it dy} {\,d} z &=& \intop\!\!\!\intop\nolimits_{\partial\! W} f{\bf F} {\,{\cdot}\,} {\bf n} {\,d} S\\[6pt] &&-\ \intop\!\!\!\intop\!\!\!\intop\nolimits_{W} f{\nabla} {\,{\cdot}\,} {\bf F} {\it {\,d} x}\, {\it dy}\, {\,d} z. \end{eqnarray*}

475

Question 8.121

Prove the identity \[ {\nabla}{\,{\cdot}\,} ({\bf F} \times {\bf G}) = {\bf G}{\,{\cdot}\,} ({\nabla}\times {\bf F}) - {\bf F} {\,{\cdot}\,} ({\nabla}\times {\bf G}). \]

Question 8.122

Show that \({\intop\!\!\!\intop\!\!\!\intop}_{W}(1/r^2)\, {\it {\,d} x}\,{\it dy}\,{\,d} z = {\intop\!\!\!\intop}_{\partial\! W}({\bf r}{\,{\cdot}\,} {\bf n}/r^2){\,d} S\), where \({\bf r} = x{\bf i} + y{\bf j} + z{\bf k}\).

Question 8.123

Fix vectors \({\bf v}_1,\ldots, {\bf v}_k \in {\mathbb R}^3\) and numbers (“charges”) \(q_1,\ldots, q_k\). Define the function \(\phi\) by \(\phi(x,y,z) = \sum_{i=1}^k q_i/(4\pi \|{\bf r} - {\bf v}_i\|)\), where \({\bf r} =(x,y,z)\). Show that for a closed surface \(S\) and \({\bf E} = - {\nabla}\phi\), \[ \intop\!\!\!\intop\nolimits_{S}{\bf E}{\,{\cdot}\,} {\,d}{\bf S}= Q, \] where \(Q\) is the total charge inside \(S\). (Assume that Gauss’ law from Theorem 10 applies and that none of the charges are on \(S\).)

Question 8.124

Prove Green’s identities \[ \intop\!\!\!\intop\nolimits_{\partial\! W} f{\nabla}g {\,{\cdot}\,} {\bf n}{\,d} S = \intop\!\!\!\intop\!\!\!\intop\nolimits_{W}(f\nabla^2 g + {\nabla}\!f{\,{\cdot}\,} {\nabla}g) {\,d} V \] and \[ \intop\!\!\!\intop\nolimits_{\partial\! W} (f{\nabla}g - g{\nabla} f) {\,{\cdot}\,} {\bf n} {\,d} S = \intop\!\!\!\intop\!\!\!\intop\nolimits_{W} (f \nabla^2 g - g\nabla^2\! f) {\,d} V. \]

Question 8.125

Suppose \({\bf F}\) satisfies div \({\bf F}=0\) and curl \({\bf F} = {\bf 0}\) on all of \({\mathbb R}^3\). Show that we can write \({\bf F} = {\nabla}\! f\), where \(\nabla^2 f = 0\).

Question 8.126

Let \(\rho\) be a continuous function on \({\mathbb R}^3\) such that \(\rho({\bf q})=0\) except for \({\bf q}\) in some region \(W\). Let \({\bf q}\in W\) be denoted by \({\bf q} = (x,y,z)\). The potential of \(\rho\) is defined to be the function \[ \phi({\bf p}) = \intop\!\!\!\intop\!\!\!\intop\nolimits_{W} \frac{\rho({\bf q})}{4\pi\|{\bf p}-{\bf q}\|} {\,d} V({\bf q}), \] where \(\|{\bf p}-{\bf q}\|\) is the distance between \({\bf p}\) and \({\bf q}\).

• (a) Using the method of Theorem 10, show that \[ \intop\!\!\!\intop\nolimits_{\partial\! W} {\nabla}\phi {\,{\cdot}\,} {\bf n} {\,d} S= -\intop\!\!\!\intop\!\!\!\intop\nolimits_W \rho{\,d} V \] for those regions \(W\) that can be partitioned into a finite union of symmetric elementary regions.
• (b) Show that \(\phi\) satisfies Poisson’s equation \[ \nabla^2\phi = -\rho. \]

[HINT: Use part (a).] (Notice that if \(\rho\) is a charge density, then the integral defining \(\phi\) may be thought of as the sum of the potential at \({\bf p}\) caused by point charges distributed over \(W\) according to the density \(\rho\).)

Question 8.127

Suppose \({\bf F}\) is tangent to the closed surface \(S= \partial\! W\) of a region \(W\). Prove that \[ \intop\!\!\!\intop\!\!\!\intop\nolimits_{W} ({\hbox{div }} {\bf F}){\,d} V= 0. \]

Question 8.128

Use Gauss’ law and symmetry to prove that the electric field due to a charge \(Q\) evenly spread over the surface of a sphere is the same outside the surface as the field from a point charge \(Q\) located at the center of the sphere. What is the field inside the sphere?

Question 8.129

Reformulate Exercise 25 in terms of gravitational fields.

Question 8.130

Show how Gauss’ law can be used to solve part (b) of Exercise 29 in Section 8.4.

Question 8.131

Let \(S\) be a closed surface. Use Gauss’ theorem to show that if \({\bf F}\) is a \(C^2\) vector field, then we have \({\intop\!\!\!\intop}_s({\nabla} \times {\bf F})\, {\cdot}\, d{\bf S} =0\).

Question 8.132

Let \(S\) be the surface of region \(W\). Show that \[ \intop\!\!\!\intop\nolimits_S {\bf r}\,{\cdot}\, {\bf n}\, dS =3 \hbox{ volume } (W). \]

Explain this geometrically.

Question 8.133

For a steady-state charge distribution and divergence-free current distribution, the electric and magnetic fields \({\bf E}(x,y,z)\) and \({\bf H}(x,y,z)\) satisfy \begin{eqnarray*} &&{\nabla}\times{\bf E}= {\bf 0},\qquad {\nabla}\,{\cdot}\, {\bf H}=0,\qquad {\nabla}\,{\cdot}\,{\bf J}=0, \qquad {\nabla}\,{\cdot}\, {\bf E}=\rho,\\ &&\qquad\hbox{and}\qquad {\nabla}\times {\bf H}={\bf J}. \end{eqnarray*}

Here \(\rho=\rho(x,y,z)\) and \({\bf J}(x,y,z)\) are assumed to be known. The radiation that the fields produce through a surface \(S\) is determined by a radiation flux density vector field, called the Poynting vector field, \[ {\bf P}={\bf E}\times{\bf H}. \]

• (a) If \(S\) is a closed surface, show that the radiation flux—that is, the flux of \({\bf P}\) through \(S\)—is given by \[ \intop\!\!\!\intop\nolimits_{S} {\bf P}\,{\cdot}\,{\,d} {\bf S}=-\intop\!\!\!\intop\!\!\!\intop\nolimits_{V}{\bf E}\,{\cdot}\, {\bf J}{\it {\,d} V}, \] where \(V\) is the region enclosed by \(S\).
• (b) Examples of such fields are \begin{eqnarray*} &&{\bf E}(x,y,z) = z{\bf j}+y{\bf k} \qquad {\rm and}\\ && \qquad {\bf H}(x,y,z) = -xy{\bf i}+x{\bf j}+yz{\bf k}. \end{eqnarray*} In this case, find the flux of the Poynting vector through the hemispherical shell shown in Figure 8.38. (Notice that it is an open surface.)
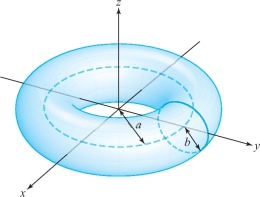
• (c) The fields of part (b) produce a Poynting vector field passing through the toroidal surface shown in Figure 8.39. What is the flux through this torus?